Dowód wprost

W trójkącie ABC dane są: kąt BAC= α oraz kąt ABC = β
(rysunek wykonaj samodzielnie)
Wykaż, że:

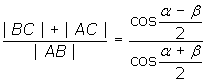
Naszym założeniem jest tu przyjęcie odpowiednich kątów, które są dane, oraz fakt, że podane kąty są kątami trójkąta (α + β + γ =180). Jeżeli ponadto oznaczymy bok BC jako a, AC jako b i AB jako c (zgodnie z zasadą nazewnictwa boków w trójkącie) otrzymamy:


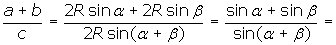
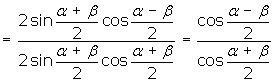
L=P, co należało dowieść.

Dowód nie wprost

Udowodnij, że 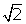jest liczbą niewymierną.
x² = 2
Załóżmy więc, że 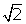jest liczbą wymierną, zatem istnieje liczba m/n, której kwadrat jest równy 2, co oznaczałoby równość:

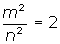
m² = 2n²
Po rozłożeniu na czynniki pierwsze obu jej stron otrzymalibyśmy czynnik 2 po prawej stronie w potędze nieparzystej, a po lewej w potędze parzystej, a zatem sprzeczność, która na podstawie dowodu nie wprost dowodzi nieistnienia liczby wymiernej spełniającej równanie x² = 2.
Zatem 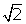jest liczbą niewymierną.

Zasada indukcji matematycznej

Udowodnij, że dla każdego n będącego liczbą naturalną dodatnią zachodzi równość:


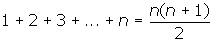
1. Sprawdzamy, że dla n=1 wzór jest prawdziwy:
L=1
P= (1*2)/2=1
L=P

2. Założenie dla n


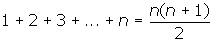
3. Teza dla n+1


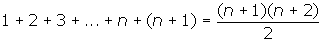
Dowód:
L = 1+2+3+...+n+n+1 =
Korzystamy z założenia:

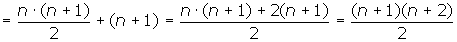
L=P
Stwierdzam, że równość ta jest prawdziwa, gdy n=1 i dla każdej dodatniej liczby naturalnej z prawdziwości równości dla n wynika jej prawdziwość dla n+1. Zatem na podstawie zasady indukcji matematycznej równość ta jest prawdziwa dla każdej dodatniej liczby naturalnej n.